Desviación estándar y error estándar
Introducción
Estándar re eviación (SD) y S Tandard mi error (SE) Son terminologías aparentemente similares; sin embargo, son conceptualmente tan variados que se usan de manera casi intercambiable en la literatura de Estadística. Ambos términos suelen ir precedidos por un símbolo más-menos (+/-) que es indicativo del hecho de que definen un valor simétrico o representan un rango de valores. Invariablemente, ambos términos aparecen con un promedio (promedio) de un conjunto de valores medidos.
Curiosamente, una SE no tiene nada que ver con estándares, errores o con la comunicación de datos científicos.
Una mirada detallada al origen y la explicación de la SD y la SE revelarán, por qué los estadísticos profesionales y los que lo usan de manera cursiva, ambos tienden a errar.
Desviación estándar (SD)
Un SD es un descriptivo Estadística que describe la propagación de una distribución. Como métrica, es útil cuando los datos se distribuyen normalmente. Sin embargo, es menos útil cuando los datos son muy sesgados o bimodales porque no describe muy bien la forma de la distribución. Normalmente, usamos SD cuando informamos las características de la muestra, porque pretendemos describir cuánto varían los datos alrededor de la media Otras estadísticas útiles para describir la dispersión de los datos son el rango intercuartil, los percentiles 25 y 75, y el rango de los datos.
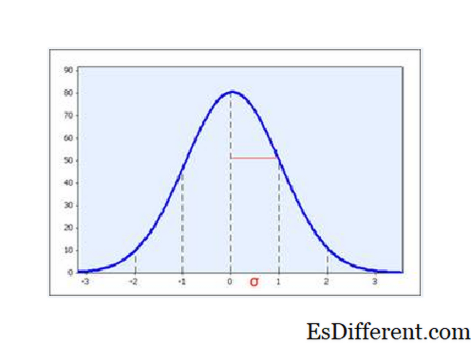
La varianza es una descriptivo La estadística también, y se define como el cuadrado de la desviación estándar. Generalmente no se informa cuando se describen los resultados, pero es una fórmula más matemáticamente manejable (a.k.a. la suma de las desviaciones al cuadrado) y desempeña un papel en el cálculo de las estadísticas.
Por ejemplo, si tenemos dos estadísticas. PAG & Q con variaciones conocidas var (PAG) & var (Q) , entonces la varianza de la suma P + Q es igual a la suma de las varianzas: var (P) + var (Q) . Ahora es evidente por qué a los estadísticos les gusta hablar de variaciones.
Pero las desviaciones estándar tienen un significado importante para la propagación, especialmente cuando los datos se distribuyen normalmente: la media del intervalo +/- 1 SD puede esperarse que capture 2/3 de la muestra, y la media del intervalo + - 2 SD Se puede esperar que capture el 95% de la muestra.
SD proporciona una indicación de hasta qué punto las respuestas individuales a una pregunta varían o "se desvían" de la media. SD le dice al investigador qué tan dispersas están las respuestas: ¿se concentran alrededor de la media o se dispersan a lo largo y ancho? ¿Todos sus encuestados calificaron su producto en la mitad de su escala o algunos lo aprobaron y otros lo rechazaron?
Considere un experimento donde se les pide a los encuestados que califiquen un producto en una serie de atributos en una escala de 5 puntos. La media para un grupo de diez encuestados (etiquetados "A" a través de "J" a continuación) para "buen valor para el dinero" fue 3.2 con un SD de 0.4 y la media para "confiabilidad del producto" fue 3.4 con un SD de 2.1.
A primera vista (considerando solo los medios), parecería que la confiabilidad se calificó por encima del valor. Pero la SD más alta para la confiabilidad podría indicar (como se muestra en la siguiente distribución) que las respuestas fueron muy polarizadas, donde la mayoría de los encuestados no tuvieron problemas de confiabilidad (calificaron el atributo con un "5"), pero un segmento más pequeño, pero importante de los encuestados, tuvo un problema de fiabilidad y calificó el atributo "1". Mirar solo la media cuenta solo una parte de la historia, sin embargo, la mayoría de las veces, esto es en lo que se enfocan los investigadores. Es importante tener en cuenta la distribución de las respuestas y el SD proporciona una valiosa medida descriptiva de esto.
| Demandado | Buen valor para el dinero | Fiabilidad del producto |
| UNA | 3 | 1 |
| segundo | 3 | 1 |
| do | 3 | 1 |
| re | 3 | 1 |
| mi | 4 | 5 |
| F | 4 | 5 |
| sol | 3 | 5 |
| H | 3 | 5 |
| yo | 3 | 5 |
| J | 3 | 5 |
| Media | 3.2 | 3.4 |
| Std. Dev. | 0.4 | 2.1 |
Primera encuesta: encuestados que califican un producto en una escala de 5 puntos
Dos distribuciones muy diferentes de respuestas a una escala de calificación de 5 puntos pueden producir la misma media. Considere el siguiente ejemplo que muestra valores de respuesta para dos calificaciones diferentes.
En el primer ejemplo (Clasificación "A"), SD es cero porque TODAS las respuestas fueron exactamente el valor medio. Las respuestas individuales no se desviaron en absoluto de la media.
En la Clasificación “B”, aunque la media del grupo es la misma (3.0) que la primera distribución, la Desviación Estándar es mayor. La desviación estándar de 1.15 muestra que las respuestas individuales, en promedio *, estaban a poco más de 1 punto de la media.
| Demandado | Calificación “A” | Calificación “B” |
| UNA | 3 | 1 |
| segundo | 3 | 2 |
| do | 3 | 2 |
| re | 3 | 3 |
| mi | 3 | 3 |
| F | 3 | 3 |
| sol | 3 | 3 |
| H | 3 | 4 |
| yo | 3 | 4 |
| J | 3 | 5 |
| Media | 3.0 | 3.0 |
| Std. Dev. | 0.00 | 1.15 |
Segunda encuesta: encuestados que califican un producto en una escala de 5 puntos
Otra forma de ver la SD es representando la distribución como un histograma de respuestas. Una distribución con una SD baja se mostraría como una forma alta y estrecha, mientras que una SD grande se indicaría con una forma más amplia.
Por lo general, la SD no indica "correcto o incorrecto" o "mejor o peor"; una SD inferior no es necesariamente más deseable. Se utiliza puramente como estadística descriptiva. Describe la distribución en relación con la media.
T Descargo de responsabilidad técnica relacionada con SD
Pensar en la SD como una "desviación de la cobertura" es una excelente manera de entender conceptualmente su significado. Sin embargo, en realidad no se calcula como un promedio (si lo fuera, lo llamaríamos la "desviación de la cobertura"). En su lugar, está "estandarizado", un método algo complejo de calcular el valor utilizando la suma de los cuadrados.
A efectos prácticos, el cálculo no es importante. La mayoría de los programas de tabulación, hojas de cálculo u otras herramientas de gestión de datos calcularán la SD para usted. Más importante es entender lo que transmiten las estadísticas.
Error estándar
Un error estándar es un inferencial estadística que se utiliza cuando se comparan medias muestrales (promedios) entre poblaciones. Es una medida de precisión de la media muestral. La media de la muestra es una estadística derivada de datos que tienen una distribución subyacente. No podemos visualizarlo de la misma manera que los datos, ya que hemos realizado un solo experimento y tenemos un solo valor. La teoría estadística nos dice que la media de la muestra (para una muestra bastante grande y en unas pocas condiciones de regularidad) se distribuye de manera aproximadamente normal. La desviación estándar de esta distribución normal es lo que llamamos el error estándar.

Cuando queremos comparar los promedios de los resultados de un experimento de dos muestras de Tratamiento A versus Tratamiento B, debemos estimar con qué precisión hemos medido los promedios.
En realidad, estamos interesados en saber con qué precisión hemos medido la diferencia entre los dos medios. Llamamos a esta medida el error estándar de la diferencia. Es posible que no se sorprenda al saber que el error estándar de la diferencia en los medios de muestra es una función de los errores estándar de los medios:

 , donde n es el número de puntos de datos.
, donde n es el número de puntos de datos.
Observe que el error estándar depende de dos componentes: la desviación estándar de la muestra y el tamaño de la muestra norte . Esto tiene un sentido intuitivo: cuanto mayor sea la desviación estándar de la muestra, menos precisos podemos ser sobre nuestra estimación de la media real.
Además, cuanto mayor sea el tamaño de la muestra, más información tenemos sobre la población y, con mayor precisión, podemos estimar la media real.
SE es una indicación de la fiabilidad de la media. Una pequeña SE es una indicación de que la media muestral es un reflejo más preciso de la media real de la población. Un tamaño de muestra más grande normalmente resultará en una SE más pequeña (mientras que SD no se ve directamente afectado por el tamaño de la muestra).
La mayoría de las investigaciones de encuestas involucran extraer una muestra de una población. Luego hacemos inferencias sobre la población a partir de los resultados obtenidos de esa muestra. Si se extrajo una segunda muestra, los resultados probablemente no coincidirán exactamente con la primera muestra. Si el valor medio para un atributo de calificación era 3.2 para una muestra, podría ser 3.4 para una segunda muestra del mismo tamaño. Si tuviéramos que extraer un número infinito de muestras (de igual tamaño) de nuestra población, podríamos mostrar las medias observadas como una distribución. Entonces podríamos calcular un promedio de todas nuestras medias muestrales. Esta media sería igual a la verdadera media de la población. También podemos calcular la desviación estándar de la distribución de medias muestrales. La SD de esta distribución de medias muestrales es el SE de cada media muestral individual.
Nosotros, así, tenemos nuestra observación más significativa: SE es el SD de la media poblacional.
| Muestra | Media |
| 1º | 3.2 |
| 2do | 3.4 |
| 3er | 3.3 |
| Cuarto | 3.2 |
| Quinto | 3.1 |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| Media | 3.3 |
| Std. Dev. | 0.13 |
Tabla que ilustra la relación entre SD y SE.
Ahora está claro que si la desviación estándar de esta distribución nos ayuda a comprender qué tan lejos está la media de una muestra de la verdadera media de la población, entonces podemos usar esto para entender qué tan precisa es la media de cada muestra individual en relación con la media real. Esa es la esencia de SE.
En realidad, solo hemos extraído una sola muestra de nuestra población, pero podemos usar este resultado para proporcionar una estimación de la confiabilidad de nuestra media observada de la muestra.
De hecho, SE nos dice que podemos estar seguros al 95% de que nuestra media observada de la muestra es más o menos aproximadamente 2 (en realidad, 1.96) Errores estándar de la media poblacional.
La siguiente tabla muestra la distribución de respuestas de nuestra primera (y única) muestra utilizada para nuestra investigación. La SE de 0.13, siendo relativamente pequeña, nos da una indicación de que nuestra media está relativamente cerca de la media real de nuestra población en general. El margen de error (con una confianza del 95%) para nuestra media es (aproximadamente) el doble de ese valor (+/- 0.26), lo que nos indica que la verdadera media es más probable entre 2.94 y 3.46.
| Demandado | Clasificación |
| UNA | 3 |
| segundo | 3 |
| do | 3 |
| re | 3 |
| mi | 4 |
| F | 4 |
| sol | 3 |
| H | 3 |
| yo | 3 |
| J | 3 |
| Media | 3.2 |
| Std. Errar | 0.13 |
Resumen
Muchos investigadores no entienden la distinción entre Desviación estándar y Error estándar, a pesar de que generalmente se incluyen en el análisis de datos. Si bien los cálculos reales para la desviación estándar y el error estándar son muy similares, representan dos medidas muy diferentes pero complementarias. SD nos informa sobre la forma de nuestra distribución, qué tan cerca están los valores de los datos individuales del valor medio. SE nos dice qué tan cerca está nuestra media muestral a la media real de la población general.Juntos, ayudan a proporcionar una imagen más completa de lo que la media puede decirnos.



